The Initial Values

The Initial (or Seed) values

The strangest part of the formula is the little "d".

PR(A) = (1-d) + d (PR(T1)/C(T1) + ... + PR(Tn)/C(Tn)) .

Simple setup with 5 pages What good does it do to multiply every page's PageRank by the same factor - and what's the purpose of adding (1-d) to every PageRank?

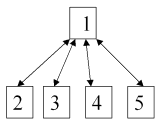
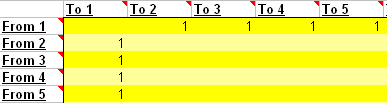
Consider the simple set-up to the left: Page1 links to all pages - and all subpages link back. This is specified on the spreadsheet like below:

Simple setup with 5 pages
How to specify the simple structure
The result can be seen on this spreadsheet. Notice that for each iteration the total PageRank for the 5 pages is 5 - so the average PageRank is 1.

Intial value 10
Initial value set to 10
Initial value -1
Initial value set to minus 1
This doesn't seem so odd at first - after all we have specified an initial PageRank of 1 for each page. Suppose we try some other "seed" values - like 10 (to the left) or even minus one (to the right). The results can be seen here and here - and notice that in both cases the average PageRank is getting closer and closer to 1.

Try the spreadsheet for different set-ups and if you have enough iterations, the average always become exactly 1 - as long as you don't have any dead ends.

So that's the purpose of adding (1-d) to every PageRank and multiplying by a dampening factor d: to ensure that the average PageRank becomes 1, or as they say at Stanford, "Note that the PageRanks form a probability distribution over web pages, so the sum of all web pages' PageRanks will be one".

Now, let's look at the value of the damping factor.